Curvas Bézier [python]

Hoxe ímos ver un pequeno truquiño para facer fácilmente curvas suaves, esta é unha técnica moi usada nos gráficos de computadores. As curvas bézier foron utilizadas xa no ano '62, por (adiviñade quén) Pierre Bézier para deseñar superficies de automobiles e, volvendo á época actual pódense atopar entre outras moitas cousas no canvas de HTML5.

Así que ímos ver como funcionan por detrás...



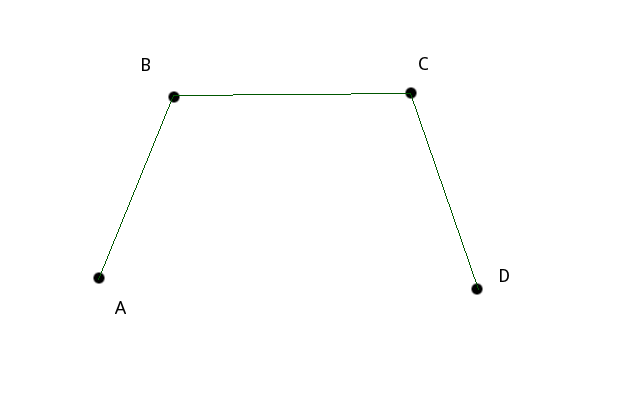
As curvas de Bézier están definidas por un conxunto arbitrario de puntos, supoñamos que temos 4 (A, B, C e D), para trazar a curva que corresponda os catro tomaremos cada par de puntos consecutivos (A-B, B-C e C-D) e trazamos unha recta entre eles.

Agora supoñamos que queremos saber onde cae o punto do primeiro cuarto da curva (segundo este método teremos que calcular cada punto individualmente), tomaremos como puntos entón o primeiro cuarto de cada liña.

Así, a ollo :P

E repetímo-lo proceso ata só quedar con un punto, que será o que corresponda a curva.

Por suposto, se non queremos pasar a vida fedellando no GIMP para debuxar a curva sempre podemos programala:

def frange(start, end, step):
    """Funciona coma un range() pero con números con decimais."""
    points = []
    next = start
    while next < end:
        points.append(next)
        next += step

    return points

def point_in_line(p1, p2, cut):
    """Toma o punto 'cut' da liña entre os puntos p1 e p2."""
    line = []
    for dim1, dim2 in zip(p1, p2):
        diff = dim2 - dim1
        line.append(dim1 + diff * cut)

    return line

def bezier(data_points, cut):
    """Calcula un punto da curva de bézier a partir do conxunto de puntos."""
    while len(data_points) > 1:
        next = []
        for i in xrange(len(data_points) - 1):
            next.append(point_in_line(data_points[i], data_points[i + 1], cut))

        data_points = next
    return data_points[0]

Así, supoñendo os puntos:

data = [(0, 2), (1.5, 2), (0.5, 0), (2, 0)]

Xeraríamos os puntos da curva bézier entre 0 e 1 cunha resolución de 0.001

points = [bezier(data, x) for x in frange(0, 1, .001)]

Para amosalos poderíamos por exemplo introducilos nun arquivo:

f = open("saída", "wt")
for point in points:
    print >> ' '.join(map(str, point))
f.close()

E debuxalos con `gnuplot`:

gnuplot -e "plot 'saída'" -p